SOAL AKM TRANSFORMASI MATRIKS

 1.  Tata mendapatkan tugas dari Yuliana untuk menentukan besaran translasi yang dilakukannya jika posisi awalnya dititik $(4,2)$ dan posisi akhirnya$(-1,-2)$  berapakah besaran translasinya?

Jawab;

Pososi Akhir = posisi awal + besaran translasi

$\left(\begin{matrix}-1\\-2\end{matrix}\right)=\left(\begin{matrix}4\\2\end{matrix}\right)+\left(\begin{matrix}a\\b\end{matrix}\right)$

$4+a=-1$ maka $a=-1-4=-5$

$2+b=-2$ maka $b=-2-2=-4$

jadi besaran translasinya $(-5,-4)$

2.  Persamaan parabola $y=2x^2+6$ ditranslasikan oleh matriks $\left(\begin{matrix}1\\3\end{matrix}\right)$ akan mempunyai bayangan parabola dengan titik puncak ….

Jawab;

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}x\\y\end{matrix}\right)+\left(\begin{matrix}1\\3\end{matrix}\right)$

$x+1=x'$ maka $x=x'-1$ .....(1)

$y+3=y'$ maka $y=y'-3$ ....(2)

substitusi (1) dan (2) ke $y=2^2+6$ menjadi $y'-3=2(x'-1)^2+6$

$y'-3=2(x'^2-2x'+1)+6$

$y'-3=2x'^2-4x'+2+6$

$y'=2x'^2-4x'+11$

bayangannya $y=2x^2-4x+11$

titik puncak untuk sumbu $x$ yaitu $x_{puncak}=-\frac{b}{2a}=-\frac{-4}{2(2)}=1$

substitusi $x=1$ ke persamaan bayagan menjadi $y=2(1)^2-4(1)+11=2-4+11=9$

jadi titik puncak bayangannya yaitu $(1,9)$

3.  Nurul ingin mempresentasikan grafik fungsi linear, dia membuat sketsa grafik terse but  menggunakan aplikasi Geogebra,Ternyata Julia dengan isengnya, menggeser grafik yang telah di buat Nurul ke arah atas sejauh 2 satuan dan ke kiri sejauh 1 satuan sehingga grafik baru tersebut (bayangannya) menjadi $3x-2y+1=0$.  Akhirnya Julia minta maaf pada Nurul. “Nurul, Maaf ya. Tadi saya menggeser grafik yang kamu buat”. Nurul menjawab “hmm, oke, saya akan memaafkan kamu, dengan syarat kamu sebutkan kembali dengan benar fungsi awal sebelum digeser tadi”. Apa jawaban Julia supaya mendapatkan maaf tersebut?

Jawab

Translasi $(-1,2)$ dan bayangannya $3x'-2y'+1=0$

Pososi Akhir = posisi awal + besaran translasi

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}x\\y\end{matrix}\right)+\left(\begin{matrix}-1\\2\end{matrix}\right)$

$x'=x-1$ ....(1)

$y'=y+2$ ....(2)

substitusi (1) dan (2) kepersamaan bayangan $3x'-2y+1=0$ menjadi $3(x-1)-2(y+2)+1=0$

$3x-3-2y-4+1=0$

$3x-2y-6=0$

jadi grafik awalnya $3x-2y-6=0

4.   

Sumber gambar: Peta - Arab Saudi (Kingdom of Saudi Arabia) - MAP[N]ALL.COM (mapnall.com)

Syahril mengatur strategi perjalananya, dia sekarang berada di Qatar, karena proses refleksi terhadap sumbu y dilanjutkan refleksi sumbu x setelah itu dia melanjutkan perjalanan menuju arah kiri sebesar satu satuan dan ke atas satu satuan. Dimanakah Syahril posisi nya setelah melakukan perjalanan tersebut?

Jawab;

Qatar terdapat pada koordinat $(5,0)$ pencerminan terhadap sumbu y $(x',y')=(-5,0)$ dilanjutkan pencerminan terhadap sumbu x $(x'',y'')=(x',-y')=(-5,0)$ lanjutkan translasi $T(-1,1)$ sehingga $(x''',y''')=(-5-1,0+1)=(-6,1)$

koordinat $(-6,1)$ berada di Algeria. 

 

5.    

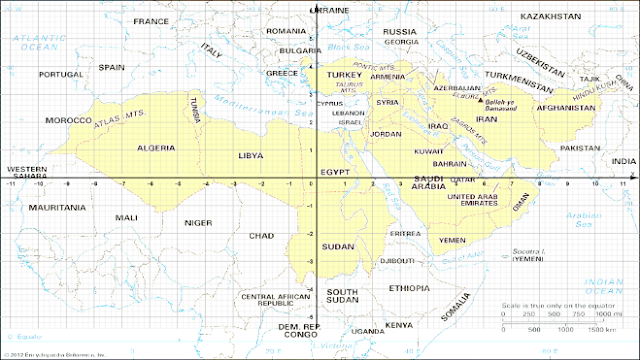
Sumber gambar: Peta - Arab Saudi (Kingdom of Saudi Arabia) - MAP[N]ALL.COM (mapnall.com)

Refleksi atau pencerminan adalah materi matematika yang sedang dipelajari Yulqi. Ketika melihat peta timur tengah, dia meletakkan sebuah titik pada koordinat $(4,1)$, bertepatan di Kuwait, Yulqi menjadikan sumbu koordinat sebagai cerminnya, sehingga dia berusaha mencari di negara mana titik tersebut berada setelah di cerminkan?

Jawab;

$(41)$ dicerminkan sumbu kooordinat sehingga bayangannya $(x',y')=(-x,-y)=(-4,-1)$. koordinat $(-4,-1)$ berada di Niger.

6.    Capten Tsubasa bermain bola kaki, ternyata bola yang ditendangnya membentuk lintasan parabola dengan fungsi $y=x^2+4x+4$, karena tendangan tersebut mudah dibaca oleh penjaga gawang, maka ia menggunakan jurus bayangan yaitu jurus pencerminan terhadap garis $x=3$. Namun penjaga gawang tersebut dapat membaca jurus yang digunakan Capten Tsubasa dan langsung mencari bayangannya. Apakah bayangan yang diperoleh penjaga gawang supaya dia bisa menangkap bola dari tendangan Capten Tsubasa tersebut?

Jawab;

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2(3)-x\\y\end{matrix}\right)=\left(\begin{matrix}6-x\\y\end{matrix}\right)$

$6-x=x'$

$-x=x'-6$

$x=-x'+6$ ........(1)

$y=y'$ ............(2)

subtitusi (1) dan (2) ke persamaan fungsi $y=x^2+4x+4$ menjadi $y'=(-x'+6)^2+4(-x'+6)+4$

$y'=(x'^2-12x'+36)-4x'+24+4$

$y'=x'^2-16x'+64$

jadi bayangannya $y=x^2-16x+64$

7.  

rajamapat.jpg (1093×630) (bp.blogspot.com)

Aldila, oca, zahra, silvi dan Tiara sedang mempresentasikan foto yang diambilnya ketika berlibur di Manokwari, tampilan pada layar seperti itu, ternyata zaki tidak dapat melihat tampilan tersebut karena dia tidak menggunakan kaca mata, salah satu solusi, tiara harus memperbesar foto tersebut degan skala 2 dengan titik pusat perbesar di (0,1). Dimakah titik sudut foto tersebut setelah di perbesar?

Jawab;

$k=2$ dan $(a,b)=(0,1)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}k&0\\0&k\end{matrix}\right)\left(\begin{matrix}x-a\\y-b\end{matrix}\right)+\left(\begin{matrix}a\\b\end{matrix}\right)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2&0\\0&2\end{matrix}\right)\left(\begin{matrix}x-0\\y-1\end{matrix}\right)+\left(\begin{matrix}0\\1\end{matrix}\right)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2&0\\0&2\end{matrix}\right)\left(\begin{matrix}x\\y-1\end{matrix}\right)+\left(\begin{matrix}0\\1\end{matrix}\right)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2(x)+0(y-1)\\0(x)+2(y-1)\end{matrix}\right)+\left(\begin{matrix}0\\1\end{matrix}\right)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2(x)\\2y-2\end{matrix}\right)+\left(\begin{matrix}0\\1\end{matrix}\right)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2(x)\\2y-3\end{matrix}\right)$

* Titik $(2,-1)$ maka $\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2(2)\\2(-1)-3\end{matrix}\right)=\left(\begin{matrix}4\\-5\end{matrix}\right)$

* Titik $(2,-4)$ maka $\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2(2)\\2(-4)-3\end{matrix}\right)=\left(\begin{matrix}4\\-11\end{matrix}\right)$

* Titik $(7,-4)$ maka $\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2(7)\\2(-4)-3\end{matrix}\right)=\left(\begin{matrix}14\\-11\end{matrix}\right)$

* Titik $(7,-1)$ maka $\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}2(7)\\2(-1)-3\end{matrix}\right)=\left(\begin{matrix}14\\-5\end{matrix}\right)$

8.  Fungsi $y=2x+1$ di lakukan dilatasi dengan besaran dilatasi $\frac{1}{3}$ dan pusat dilatasi $(0,0)$ sehingga bayangannya berbentuk $ay=bx+c$. Tentukan nilai dari $a+b+c$ adalah …

Jawab;

$k=\frac{1}{3}$ dan $(a,b)=(0,0)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}k&0\\0&k\end{matrix}\right)\left(\begin{matrix}x-a\\y-b\end{matrix}\right)+\left(\begin{matrix}a\\b\end{matrix}\right)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}\frac{1}{3}&0\\0&\frac{1}{3}\end{matrix}\right)\left(\begin{matrix}x-0\\y-0\end{matrix}\right)+\left(\begin{matrix}0\\0\end{matrix}\right)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}\frac{1}{3}&0\\0&\frac{1}{3}\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)$

$\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}\frac{1}{3}x\\ \frac{1}{3}y\end{matrix}\right)$

$\frac{1}{3}x=x'$ maka $x=3x'$ ........(1)

$\frac{1}{3}y=y'$ maka $y=3y'$ ........(2)

substitusi (1) dan (2) ke $y=2x+1$ menjadi $3y'=2(3x')+1$

$3y'=6x'+1$ sehingga $a=3, b=6, c=1$ maka $a+b+c=3+6+1=10$

9.  Titik $(2,1)$dirotasikan sebesar$90^o$ dengan pusat $(0,0)$. Bayangan titik tersebut adalah …

10.  Titik $(3,2)$ dirotasikan sebesar $90^o$ searah dengan jarum jam dengan pusat (0,0). Bayangan titik tersebut adalah …

11.  Fadil meletakkan sekilo buah mangga pada titik $(3,4)$setelah ia pergi dan bardan memindahkan mangga tersebut menggunakan matriks transformasi $\left(\begin{matrix}2&5\\-2&-1\end{matrix}\right)$ setelah itu Bardan juga pergi dan Abdul memindahkan lagi mangga yang sudah dipindahkan Bardan dengan matriks tansformasinya $\left(\begin{matrix}0&2\\3&1\end{matrix}\right)$. Dimakah posisi mangga setelah dipindahkan Abdul?