Skip to main content

Pengertian, Besar dan panjang vektor.

By

 Vektor merupakan suatu besaran yang mempunyai besar (nilai) dan arah. vektor dapat disimbolkan

1.  Menggunakan huruf kecil seperti $a$

2.  Menggunakan huruf kecil dibubuhi tanda panah diatasnya seperto $\overrightarrow{a}$

3.  Menggunakan huruf kecil dibubuhi garis lurus diatasnya, seperti $\overline{a}$ 

4.  Menggunakan huruf kecil dibubuhi garis lurus dibawahnya, seperti $\underline{a}$

5.  Menggunakan penggabungan dua titik, Misalnya titik pangkalnya A dan titik ujungnya B maka dapat ditulis $\overrightarrow{AB}$.

Contoh 1;


Tentukan;

1.  $\overrightarrow{AB}$

2.  $\overrightarrow{CD}$

3.  $\overrightarrow{EF}$

4.  $\overrightarrow{GI}$

5.  vektor manakah yang sama dengan vektor $\overrightarrow{AB}$

Jawab;

$\overrightarrow{AB}$ artinya titik  pangkalya A dan titik ujung B.

1.  $\overrightarrow{AB}= titik   ujung - titik   pangkal$ 

     $\overrightarrow{AB}=B-A=\left(\begin{matrix}3\\4\end{matrix}\right)-\left(\begin{matrix}1\\1\end{matrix}\right)=\left(\begin{matrix}3-1\\4-1\end{matrix}\right)=\left(\begin{matrix}2\\3\end{matrix}\right)$

2.  $\overrightarrow{CD}$ artinya titik awalnya C dan titik ujungnya D.

     $\overrightarrow{CD}=D-C=\left(\begin{matrix}3\\1\end{matrix}\right)-\left(\begin{matrix}5\\4\end{matrix}\right)=\left(\begin{matrix}3-5\\1-4\end{matrix}\right)=\left(\begin{matrix}-2\\-3\end{matrix}\right)$

3.  $\overrightarrow{EF}$ artinya titik awalnya E dan titik ujungnya F
     $\overrightarrow{EF}=F-E=\left(\begin{matrix}5\\1\end{matrix}\right)-\left(\begin{matrix}3\\-2\end{matrix}\right)=\left(\begin{matrix}5-3\\1+2\end{matrix}\right)=\left(\begin{matrix}2\\3\end{matrix}\right)$

4.   $\overrightarrow{GH}$ artinya titik awalnya G dan titik ujungnya H

      $\overrightarrow{GH}= H- G=\left(\begin{matrix}7\\0\end{matrix}\right)-\left(\begin{matrix}5\\3\end{matrix}\right)=\left(\begin{matrix}7-5\\0-3\end{matrix}\right)=\left(\begin{matrix}2\\-3\end{matrix}\right)$

5.  Vektor $\overrightarrow{AB}=\overrightarrow{EF}$ karena memiliki nilai yang sama dan arah yang sama.
     Vektor $\overrightarrow{AB}\neq \overrightarrow{CD}$ karena memiliki nilai yang berbeda dan arah yang berbeda.
    $-(\overrightarrow{CD})=\overrightarrow{DC}$,  tanda negatif (-) pada vektor $\overrightarrow{CD}$ menyatakan perubahan arah titik awal menjadi D dan titik ujung C yang ditulis $\overrightarrow{DC}$ .

Latihan 1;


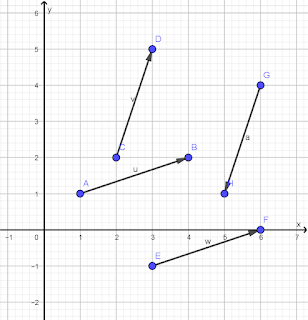
Tentukan;

1.  $\overrightarrow{AB}$
2.   $\overrightarrow{CD}$
3.  $\overrightarrow{EF}$
4.  $\overrightarrow{GI}$
5.  Tuliskan vektor yang memiliki nilai dan arah yang sama.

Panjang Vektor
Misalkan titik $A(x_A, y_A)$ dan titik $B(x_B, y_B)$ maka panjang vektor $\overrightarrow{AB}$ dapat dilulis $|\overrightarrow{AB}|$ dengan rumus;
$|\overrightarrow{AB}|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$

Contoh 2;
Diketahui titik $O(0,0),A(-1,2), B(3,4), C(5,-2)$, tentukan;
1.  Panjang vektor $\overrightarrow{OA}$
2.  Panjang vektor $\overrightarrow{BC}$
3.  Panjang vektor $\overrightarrow{CB}$
Jawab:
1.  Panjang vektor $\overrightarrow{OA}$ 
     $|\overrightarrow{OA}|=\sqrt{(x_A-x_O)^2+(y_A-y_O)^2}$
     $|\overrightarrow{OA}|=\sqrt{(-1-0)^2+(2-0)^2}$
     $|\overrightarrow{OA}|=\sqrt{(-1)^2+(2)^2}$
     $|\overrightarrow{OA}|=\sqrt{1+4}=\sqrt{5}$

2.  Panjang vektor $\overrightarrow{BC}$
     $|\overrightarrow{BC}|=\sqrt{(x_C-x_B)^2+(y_C-y_B)^2}$
     $|\overrightarrow{BC}|=\sqrt{(5-3)^2+(-2-4)^2}$
     $|\overrightarrow{BC}|=\sqrt{(2)^2+(-6)^2}$
     $|\overrightarrow{BC}|=\sqrt{4+36}$
     $|\overrightarrow{BC}|=\sqrt{40}=\sqrt{4\times10}=2\sqrt{10}$

3.  Panjang vektor $\overrightarrow{CB}$
     $|\overrightarrow{CB}|=\sqrt{(x_B-x_C)^2+(y_B-y_C)^2}$
     $|\overrightarrow{CB}|=\sqrt{(3-5)^2+(4-(-2))^2}$
     $|\overrightarrow{CB}|=\sqrt{(-2)^2+(6)^2}$
     $|\overrightarrow{CB}|=\sqrt{4+36}$
     $|\overrightarrow{CB}|=\sqrt{40}=\sqrt{4\times 10}=2\sqrt{10}$

Latihan 2
Diketahui titik $O(0,0), A(3,-5), B(-4,-1) dan C(2,-2)$, tentukan;
1.  Panjang vektor $\overrightarrow{OB}$
2.  Panjang vektor $\overrightarrow{BA}$
3.  Panjang vektor $\overrightarrow{AC}$
Labels:

Comments

Post a Comment

Popular posts from this blog

Pecatur A, B, C dan D bertanding dalam suatu turnamen catur, Urutan pemain yang memperoleh nilai tertinggi sampai ke terendah adalah ...

By
  Pecatur A, B, C dan D bertanding dalam suatu turnamen catur. Setiap pemain saling bertemu satu kali. pada setiap pertandingan, pemain yang menang, seri dan kalah, berturut-turut mendapatkan nilai 2, 1, dan 0. Data hasil pertandingan adalah A menang 2 kali, B seri dua kali, C kalah dua kali, dan D tidak pernah seri. Pembahasan; dari tabel setiap pecatur bertanding sebanyak tiga kali; seperti A dengan B, A dengan C dan A dengan D.  *B dua kali seri pastinya B  seri ketika melawan A dan melawan C (karena D tidak pernah seri),  * A menang 2 kali pastinya A menang melawan C dan melawan D ( karena A melawan B seri) *  kalah 2 kali pastinya C kalah melawan A dan melawan D (karena C seri melawan B) B dan D belum ditentukan menang atau kalah nya.   Pertandingan     Menang     seri     kalah                 A dan B         -   B/A     -      A dan C        A    -   C      A dan D       A    -     D      B dan C        -   B/C     -      B dan D      B/D    -   B/D    ?      C dan D        D
Post a Comment
Read more

SOAL AKM TRANSFORMASI MATRIKS

By
 1.   Tata mendapatkan tugas dari Yuliana untuk menentukan besaran translasi yang dilakukannya jika posisi awalnya dititik $(4,2)$ dan posisi akhirnya$(-1,-2)$  berapakah besaran translasinya? Jawab; Pososi Akhir = posisi awal + besaran translasi $\left(\begin{matrix}-1\\-2\end{matrix}\right)=\left(\begin{matrix}4\\2\end{matrix}\right)+\left(\begin{matrix}a\\b\end{matrix}\right)$ $4+a=-1$ maka $a=-1-4=-5$ $2+b=-2$ maka $b=-2-2=-4$ jadi besaran translasinya $(-5,-4)$ 2.   Persamaan parabola $y=2x^2+6$ ditranslasikan oleh matriks $\left(\begin{matrix}1\\3\end{matrix}\right)$ akan mempunyai bayangan parabola dengan titik puncak …. Jawab; $\left(\begin{matrix}x'\\y'\end{matrix}\right)=\left(\begin{matrix}x\\y\end{matrix}\right)+\left(\begin{matrix}1\\3\end{matrix}\right)$ $x+1=x'$ maka $x=x'-1$ .....(1) $y+3=y'$ maka $y=y'-3$ ....(2) substitusi (1) dan (2) ke $y=2^2+6$ menjadi $y'-3=2(x'-1)^2+6$ $y'-3=2(x'^2-2x'+1)+6$ $y'-3=2x'^2-4x'
1 comment
Read more

SOAL AKM MATRIKS

By
  7.   Jawab; a. BENAR B. Salah (seharusnya sama dengan g bukan h) C. Salah (seharusnya kotak silang bukan kotak dua) D. Salah E.  Salah 8.   Jawab; $A_{2\times 2} \times B_{2\times 2}$ karena banyak kolom A sama dengan banyak baris B (dapat dikalikan)  $B_{2\times 2} \times A_{2\times 2}$ karena banyak kolom B sama dengan banyak baris A (dapat dikalikan) $A_{2\times 2} \times C_{3\times 2}$ karena banyak kolom A tidak sama dengan banyak baris C (tida dapat dikalikan) $C_{3\times 2} \times A_{2\times 2}$ karena banyak kolom C sama dengan banyak baris A (dapat dikalikan) $B_{2\times 2} \times C_{3\times 2}$ karena banyak kolom B tidak sama dengan banyak baris C ( tidak dapat dikalikan) $C_{3\times 2} \times B_{2\times 2}$ karena banyak kolom A sama dengan banyak baris B (dapat dikalikan) jadi banyak perkalian yang dapat dilakukan adalah 6 9.   Matriks $L=\left(\begin{matrix}a&b&c\\1&2&3\\d&e&f\end{matrix}\right)$, jika $L^T$ merupakan transpose dari matriks L, ma
Post a Comment
Read more